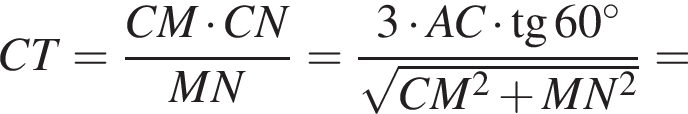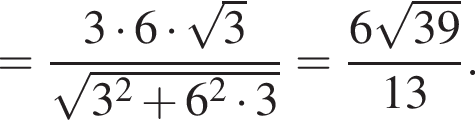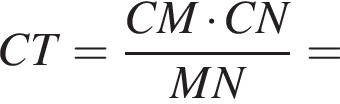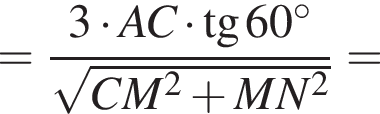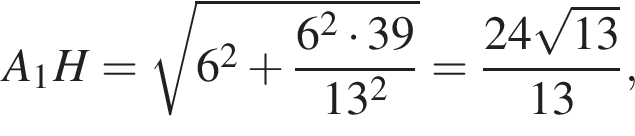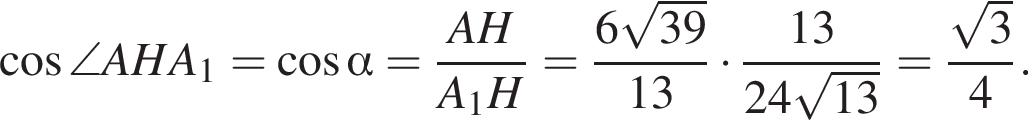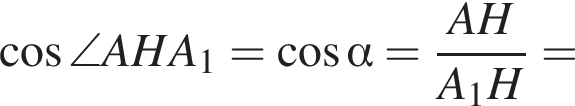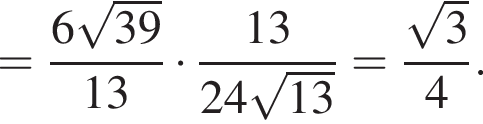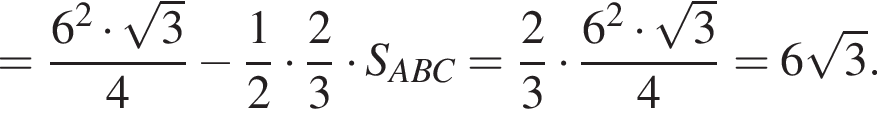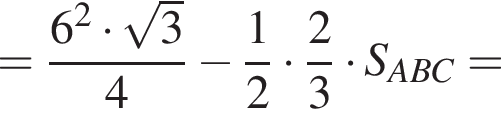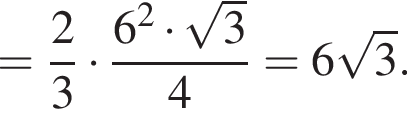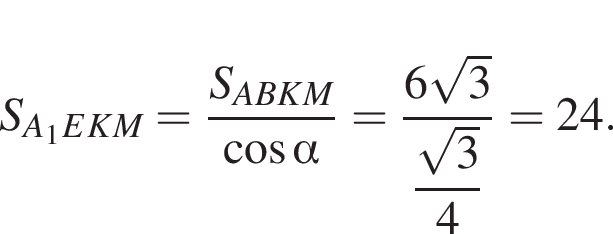Укажите номер выражения, которое является суммой двух последовательных натуральных чисел, меньшее из которых равно a.
Одно число меньше другого на 64, что составляет 16% большего числа. Найдите меньшее число.
Значение выражения 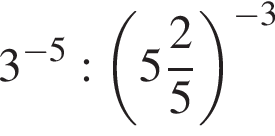 равно:
равно:
Точка С делит отрезок АВ в отношении 5 : 3, считая от точки А. Если длина отрезка АВ равна 24, то длина отрезка СВ равна:
Результат упрощения выражения 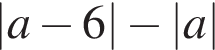 при
при 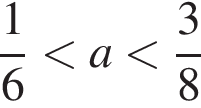 имеет вид:
имеет вид:
Площадь параллелограмма равна ![]() его стороны равны 6 и 4. Найдите большую диагональ параллелограмма.
его стороны равны 6 и 4. Найдите большую диагональ параллелограмма.
Cумма первых четырех членов геометрической прогрессии равна 60, знаменатель прогрессии равен 2. Найдите второй член геометрической прогрессии.
Для неравенства (8 − x)(x + 3) ≥ 0 укажите номера верных утверждений.
1) Число 0 не является решением неравенства;
2) неравенство равносильно неравенству 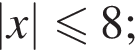
3) количество всех целых решений неравенства равно 12;
4) неравенство верно при x ∈ [−2; 3];
5) решением неравенства является промежуток [−8; 3].
Бокал имеет форму конуса. В него налита вода на высоту, равную 4. Если в бокал долить воды объемом, равным одной четвертой объема налитой воды, то вода окажется на высоте, равной:
Результат упрощения выражения 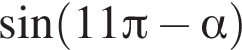 равен:
равен:


Сумма корней (или корень, если он один) уравнения 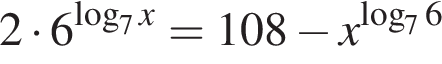 равна ...
равна ...
В окружность радиусом 6 вписан треугольник, длины двух сторон которого равны 6 и 10. Найдите длину высоты треугольника, проведенной к его третьей стороне.
Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 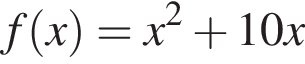 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [6; 9].
3. Максимум функции равен 25.
4. Минимальное значение функции равно -25.
5. 
6. Функция принимает отрицательные значения при 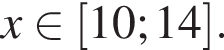
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Внутренний угол правильного многоугольника равен 135°. Выберите все верные утверждения для данного многоугольника.
1. Многоугольник является восьмиугольником.
2. В многоугольнике 40 диагоналей.
3. Если сторона многоугольника равна 2, то радиус вписанной окружности равен 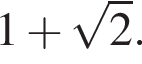
4. Площадь многоугольника со стороной a можно вычислить по формуле 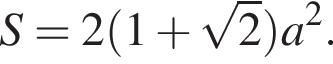
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
На диаграмме показано количество всех покупателей интернет-магазина (П) и количество покупателей, совершивших более одной покупки (ПБ), за период шесть месяцев (с июля по декабрь). Установите соответствие между вопросами А−В и ответами 1−6.
A) В каком месяце количество всех покупателей было наибольшим?
Б) В каком месяце количество покупателей, совершивших более одной покупки, было 160?
В) В каком месяце количество покупателей, совершивших более одной покупки, составило 20% от количества всех покупателей в этом месяце?
1) Июль
2) Август
3) Сентябрь
4) Октябрь
5) Ноябрь
6) Декабрь
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например, А1Б1В4.
Пусть (x;y) — целочисленное решение системы уравнений
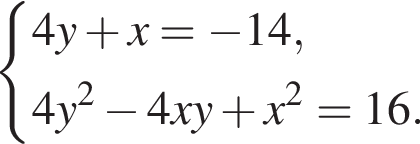
Найдите сумму x+y.
Найдите сумму корней уравнения
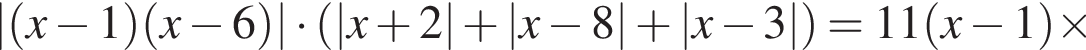
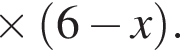
Найдите сумму целых решений неравенства 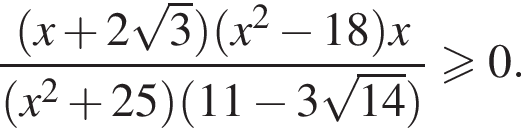
В трапеции ABCD с основаниями AD > BC точка пересечения ее диагоналей делит диагональ AC на отрезки 6 и 4. Найдите площадь трапеции, если площадь треугольника ABC равна 20.
АС — общая гипотенуза прямоугольных треугольников ABC и ADC. Плоскости этих треугольников взаимно перпендикулярны. Найдите квадрат длины отрезка BD, если 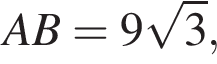
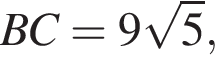 AD = DC.
AD = DC.
Найдите наименьшее целое решение неравенства

Найдите произведение всех корней (корень, если он единственный) уравнения
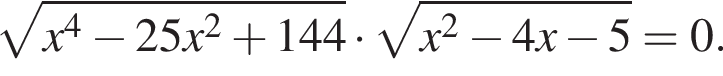
На рисунке изображен график функции 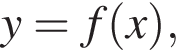 заданной на промежутке
заданной на промежутке 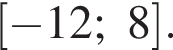 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 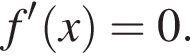 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 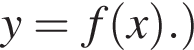
Найдите значение выражение 
Пусть 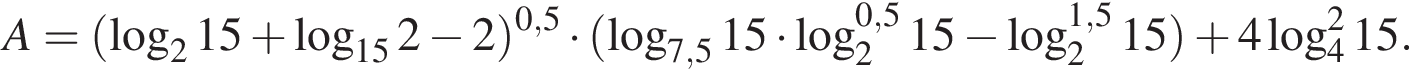
Найдите значение выражения 2A.
Найдите (в градусах) сумму корней уравнения  на промежутке (110°; 170°).
на промежутке (110°; 170°).
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 1, высота пирамиды — 3. Найдите площадь S поверхности куба. В ответ запишите значение выражения 8S.
Найдите произведение наибольшего целого решения на количество всех натуральных решений неравенства 
ABCA1В1С1 — правильная треугольная призма, у которой сторона основания и боковое ребро имеют длину 6. Через середины ребер АС и BB1 и вершину A1 призмы проведена секущая плоскость. Найдите площадь сечения призмы этой плоскостью.

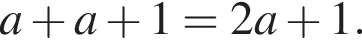
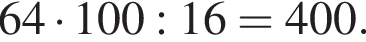 Таким образом, меньшее число
Таким образом, меньшее число 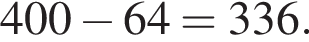
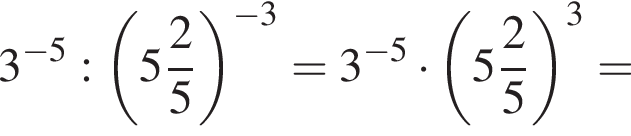
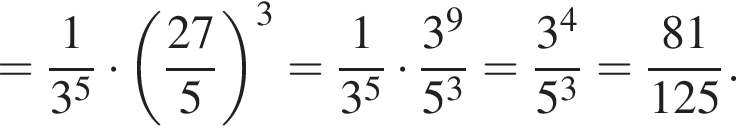
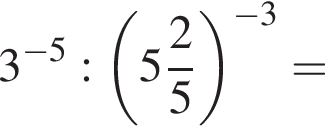
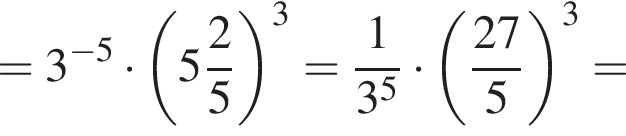
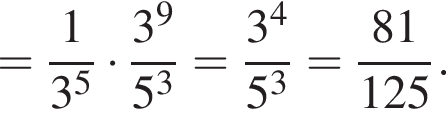
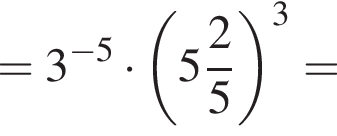
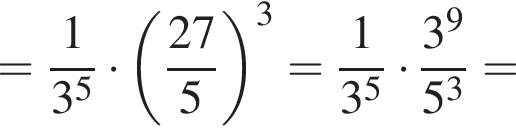
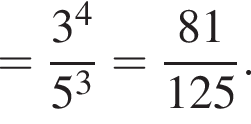
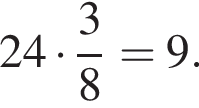



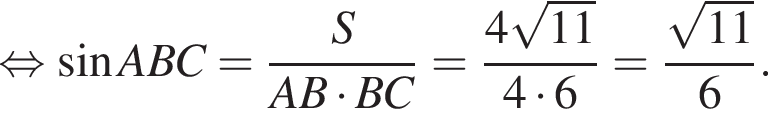
 заметив, что угол ABC тупой:
заметив, что угол ABC тупой: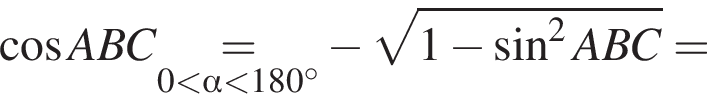
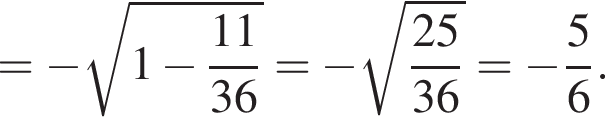
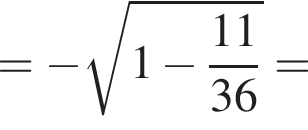
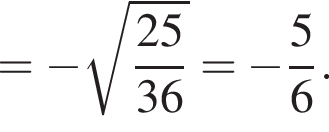
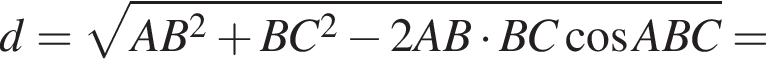
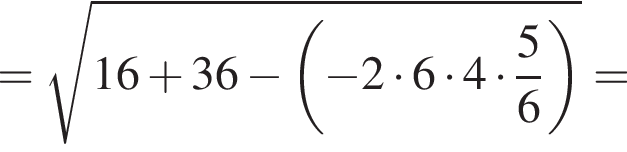


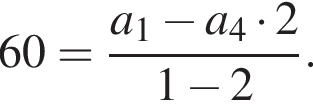 Подставим формулу четвертого члена
Подставим формулу четвертого члена 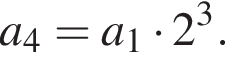 Имеем:
Имеем: 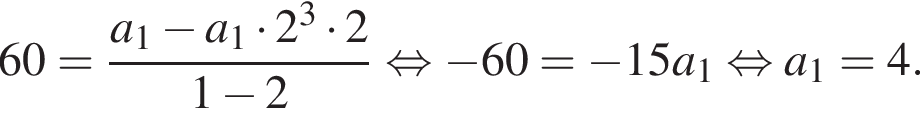
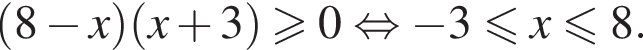
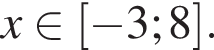 Таким образом, верные утверждения указаны под номерами 3 и 4.
Таким образом, верные утверждения указаны под номерами 3 и 4.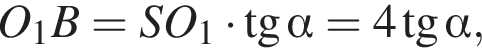
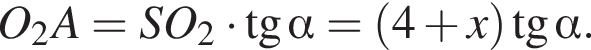 Выразим объем воды, налитой в бокал:
Выразим объем воды, налитой в бокал: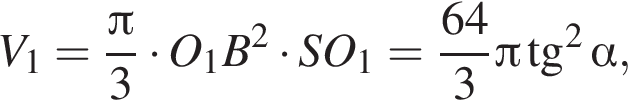
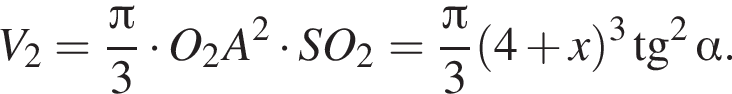
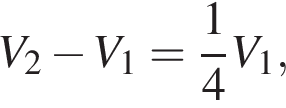 получаем, что
получаем, что 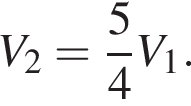 Имеем:
Имеем: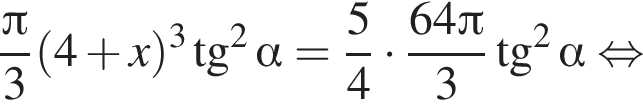
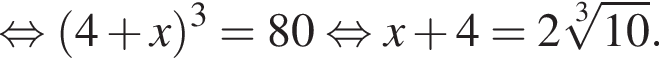
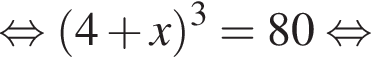
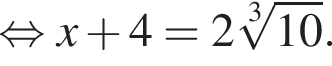

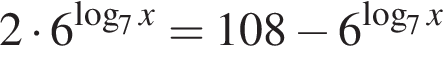
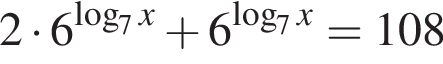
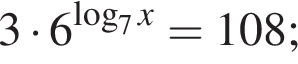
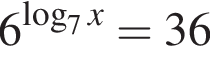
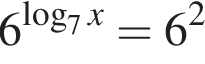
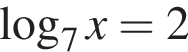
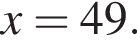
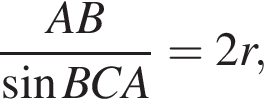 откуда
откуда 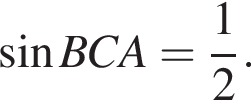 Из прямоугольного треугольника BHC имеем:
Из прямоугольного треугольника BHC имеем: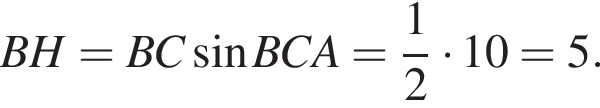
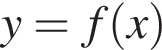 при
при 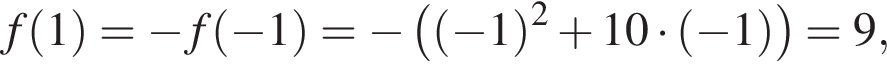
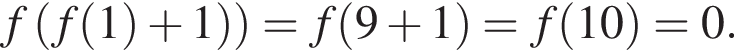 Утверждение 5 верно.
Утверждение 5 верно.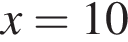 функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 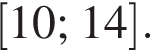 Утверждение 6 неверно.
Утверждение 6 неверно.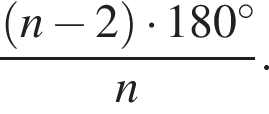 Тогда
Тогда 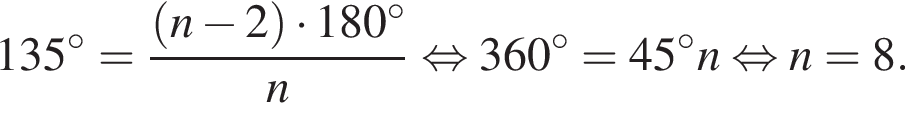
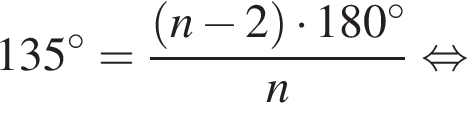
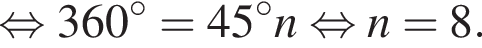
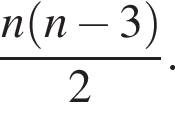 При n = 8, получаем, что диагоналей 20. Второе утверждение неверно.
При n = 8, получаем, что диагоналей 20. Второе утверждение неверно.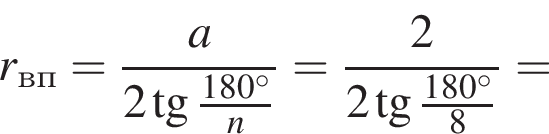
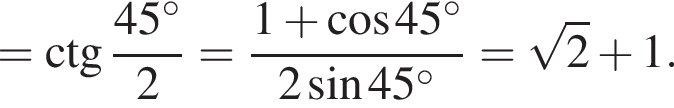
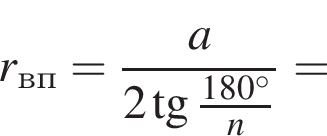
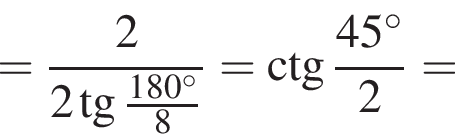
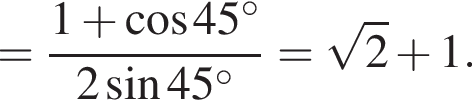
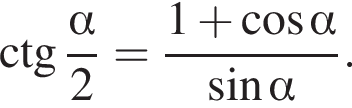
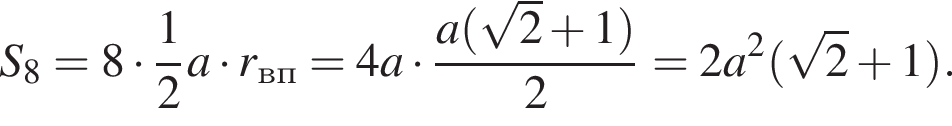
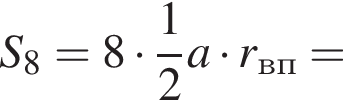
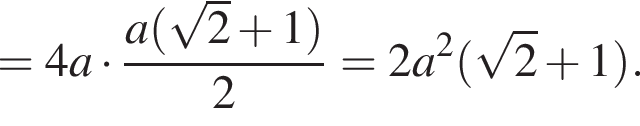
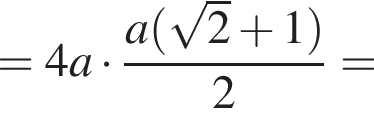
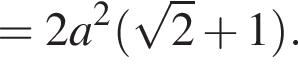
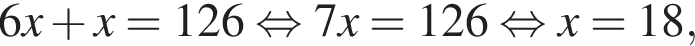
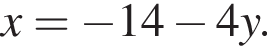 Заметим, что
Заметим, что 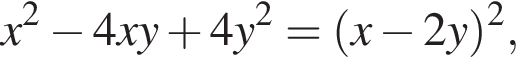 поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим: 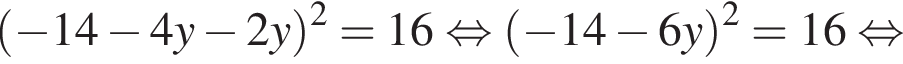
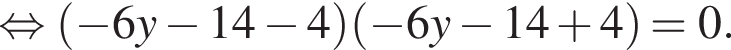
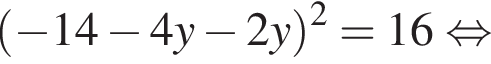
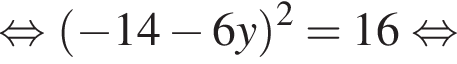
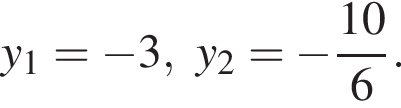 Поскольку по условию задачи требуются целочисленные решения системы, тогда найдем x:
Поскольку по условию задачи требуются целочисленные решения системы, тогда найдем x: 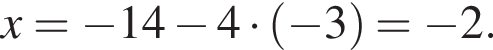 Сумма x+y равна:
Сумма x+y равна: 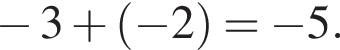

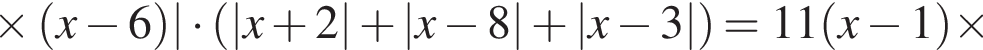
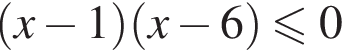 :
: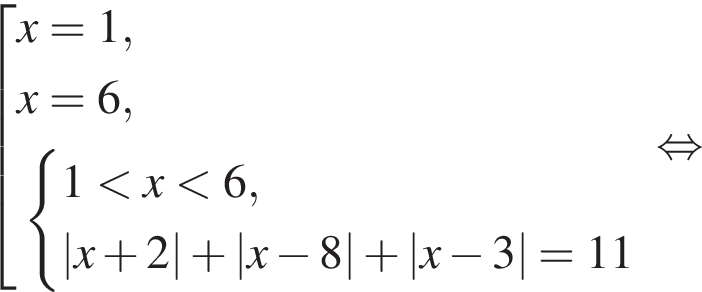
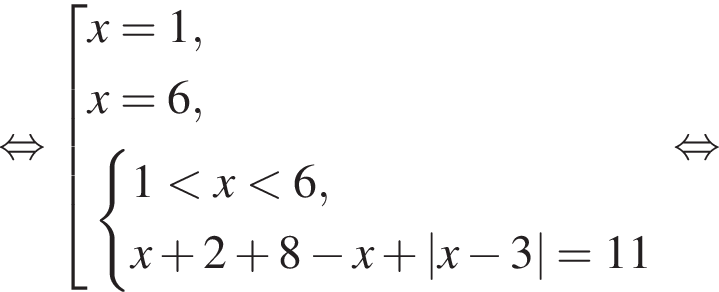
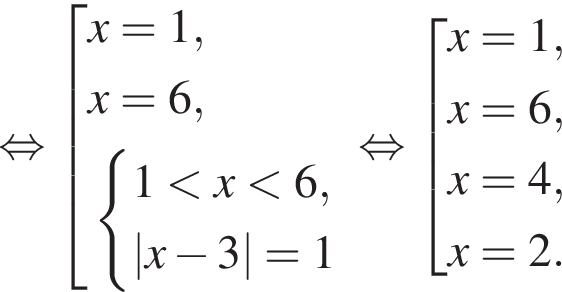
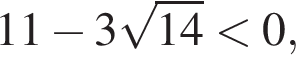 поскольку
поскольку 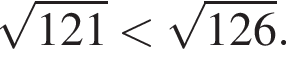 Число,
Число, 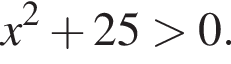 Домножим неравенство на эти числа, поменяв знак, и решим его.
Домножим неравенство на эти числа, поменяв знак, и решим его.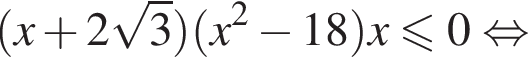
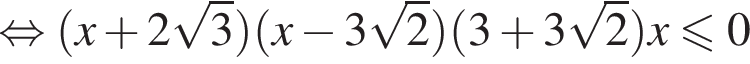
 Целыми решениями неравенства являются числа −4, 0, 1, 2, 3, 4, их сумма равна 6.
Целыми решениями неравенства являются числа −4, 0, 1, 2, 3, 4, их сумма равна 6.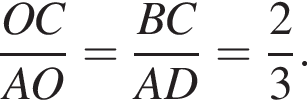
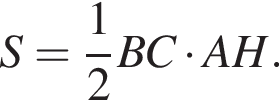 Тогда
Тогда 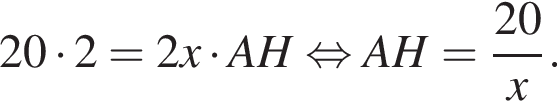 Таким образом,
Таким образом, 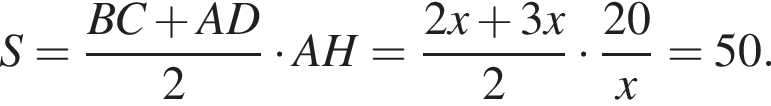
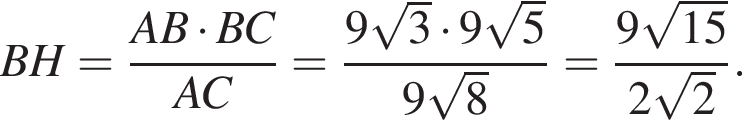
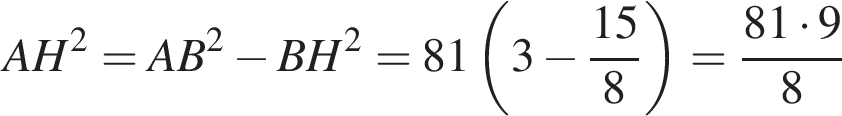
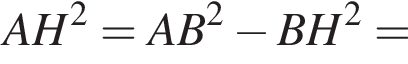
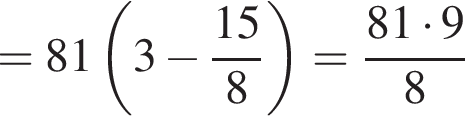
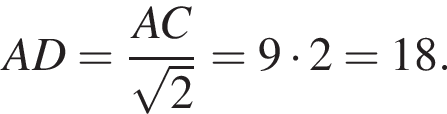
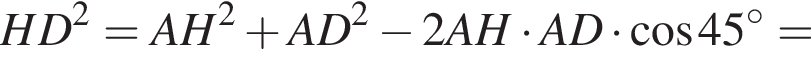
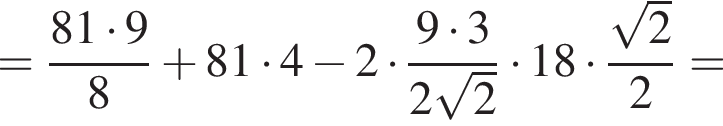
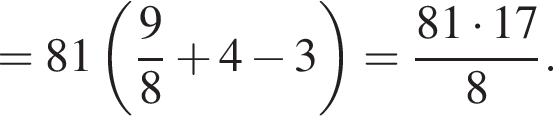


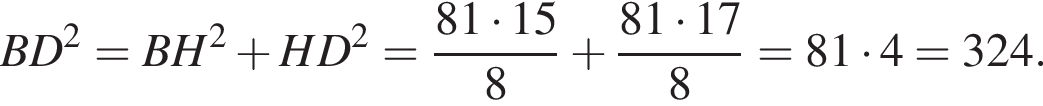

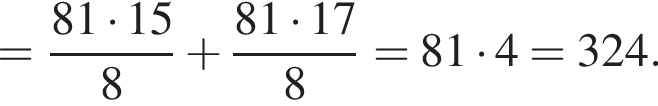
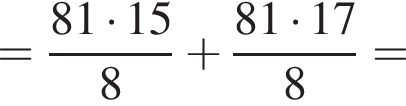
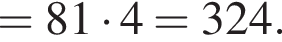
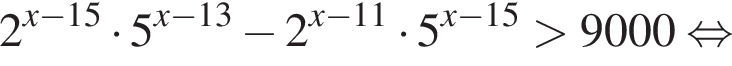
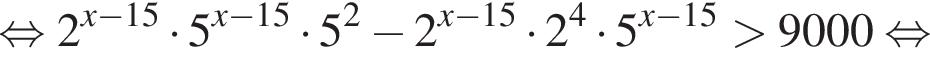

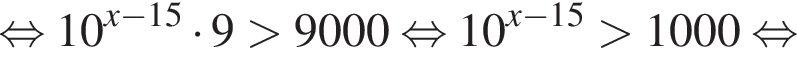
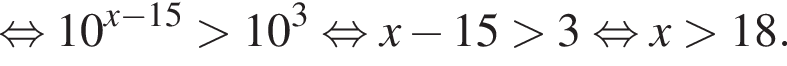
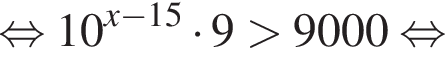

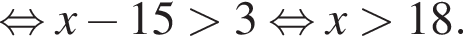
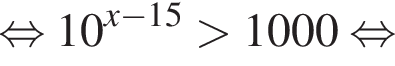
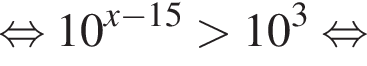
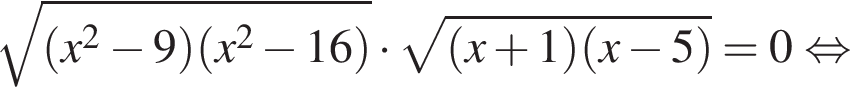
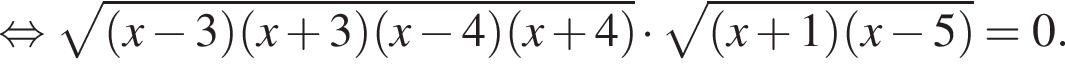
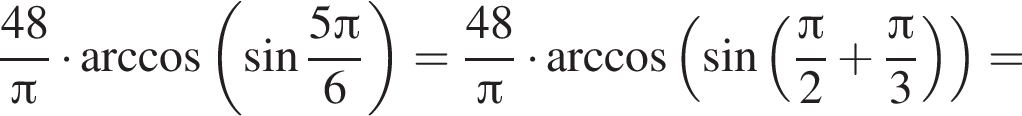
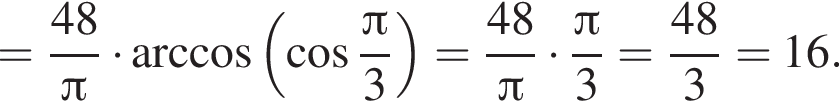
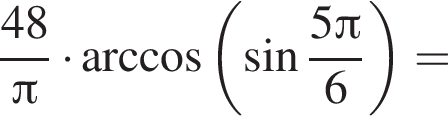
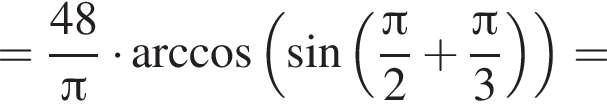
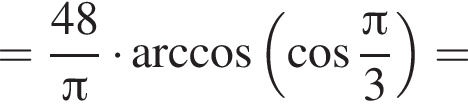
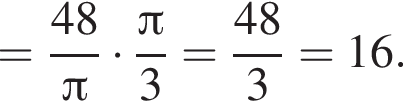

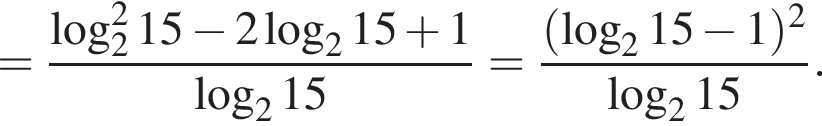
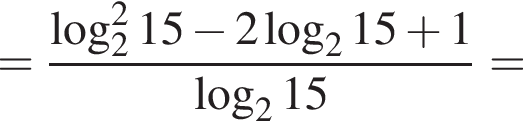
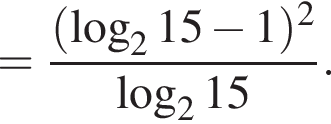
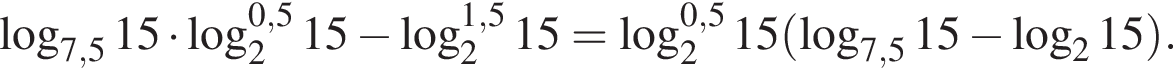
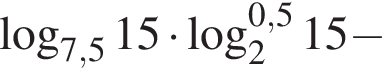
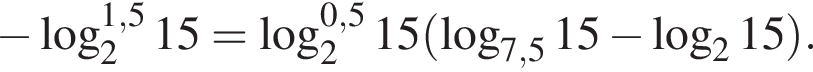
 Тогда имеем:
Тогда имеем: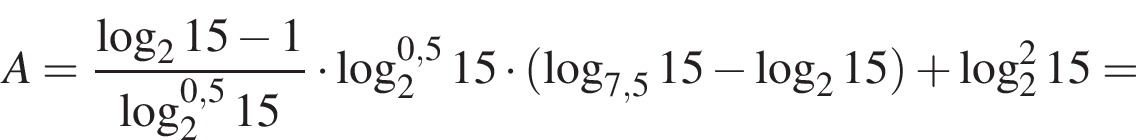
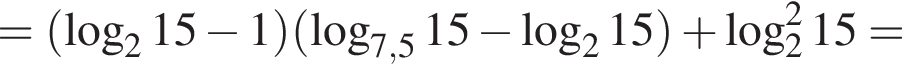
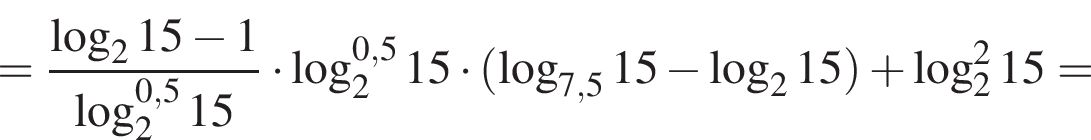
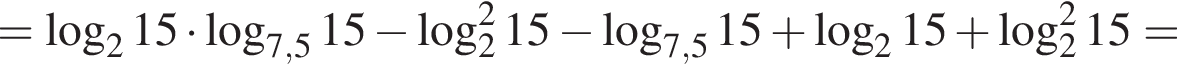
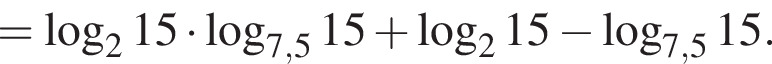
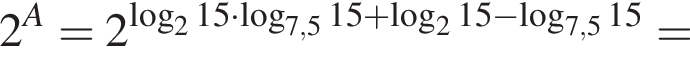
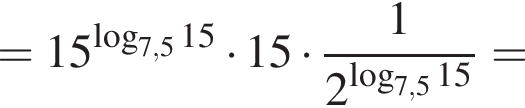
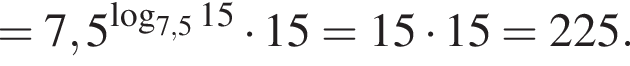
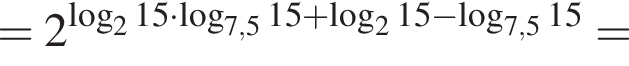
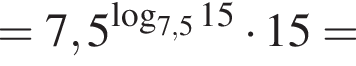
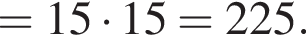
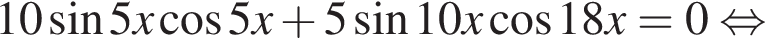
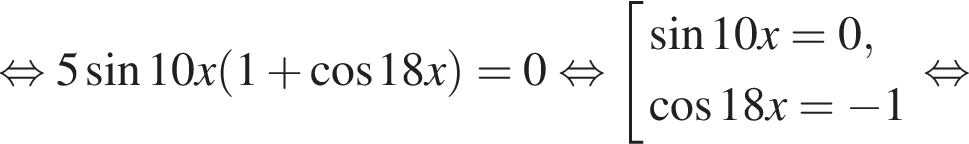
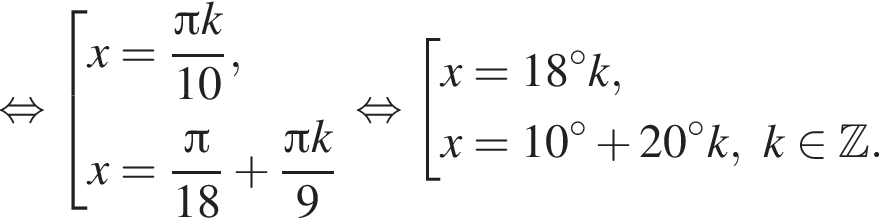
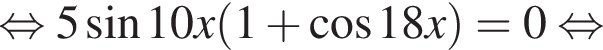
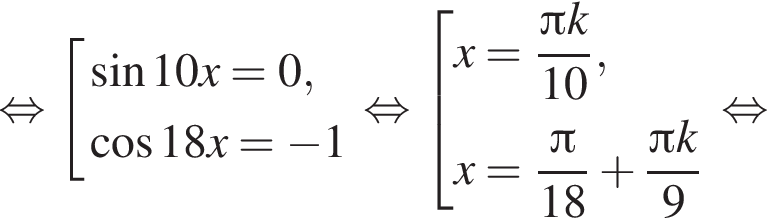
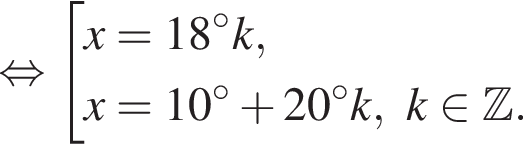
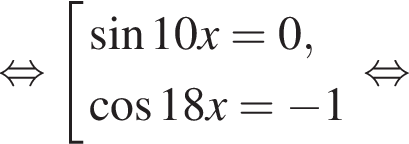
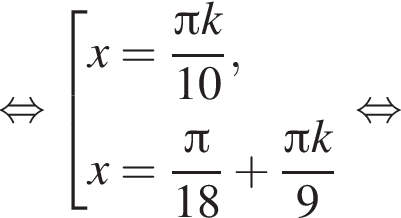
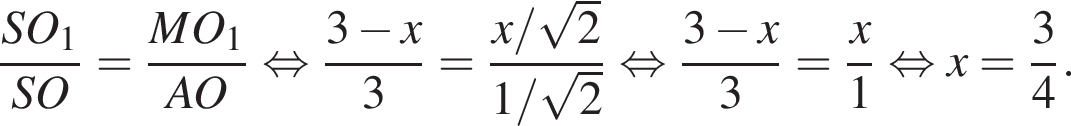
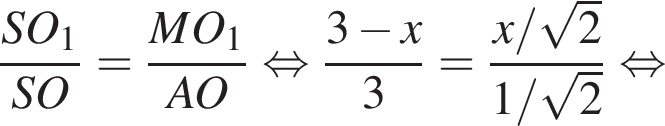
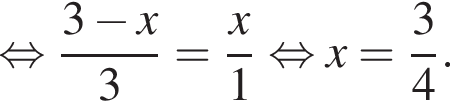
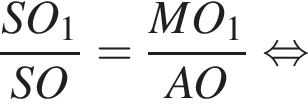
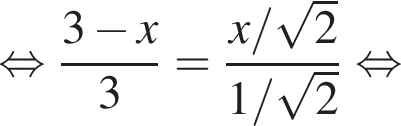
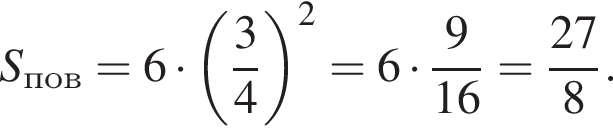
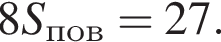
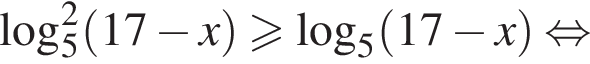
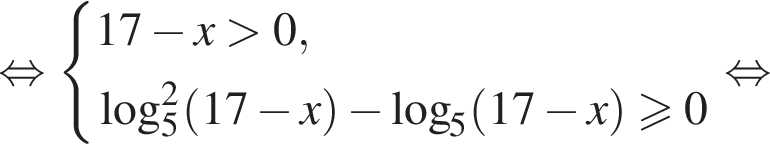
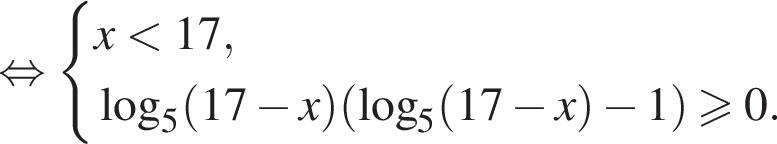
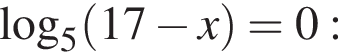
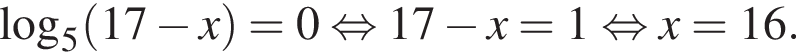
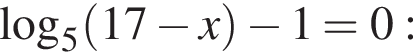

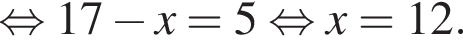
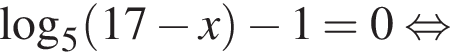
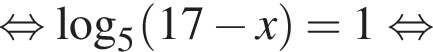
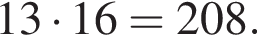
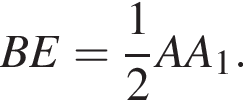 Отрезки CB и NM есть медианы треугольника ACN, поэтому CK : KB = 2 : 1, то есть CK = 4, BK = 2.
Отрезки CB и NM есть медианы треугольника ACN, поэтому CK : KB = 2 : 1, то есть CK = 4, BK = 2.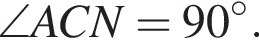 Тогда
Тогда 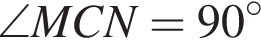 и
и